MoE: FFN -> Gate[FFNs] 起源论文: Adaptive Mixture of Local Experts
MoE 包含两个关键部分
- 专家一般是FFN
- 使用门控或者路由选择专家 (按token分发)
Sparsity
门控网络 $G$ 与 专家计算 $E$
稀疏模型往往更适合使用较小的批量大小和较高的学习率
$$ y = \sum_{i=1}^nG(x)_iE_i(x) $$
经典门控 : $G_\sigma(x)=\text{Softmax}(x\cdot W_g)$
Shazeer 提出带噪声TopK门控 能够减少计算量
$$ H(x)_i = (x\cdot W_g)_i + \text{StandardNormal}\cdot\text{Softplus}((x\cdot W_{noise})_i) $$
KeepTopK 保留 TopK 元素的值
$$ G(x) = \text{Softmax}(\text{KeepTopK}(H(x),k)) $$
Load balance
GShard
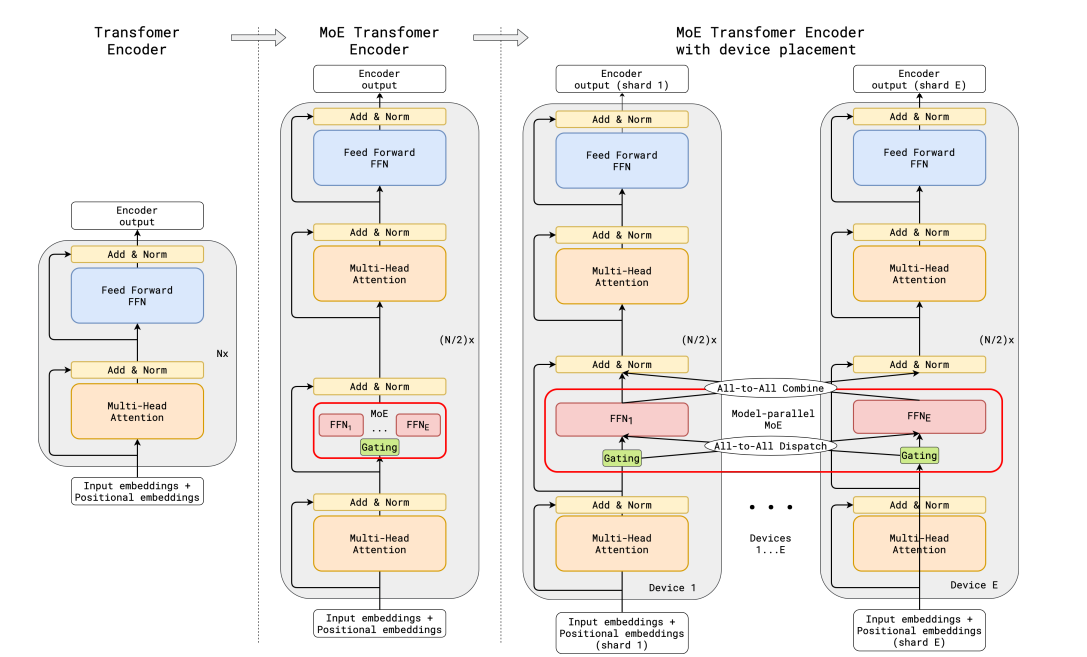
- GShard 替换 FFN 为 Top2 MoE
- MoE 共享 其他层复制
关键设置
- 辅助损失 (aux_loss) $\mathcal{L}_{aux} = \frac{1}{E}\sum^E_{e=1}\frac{c_e}{S}\cdot m_e$
- $c_e$ 表示专家处理量
- $m_e$ 表示专家门控概率 (mean of logits)
- 用 $m_e$ 替代 $c_e/S$ 使得可以梯度更新
- 随机路由 (top2) 最高+权重采样
- 专家容量 限制专家处理数量 溢出的可能丢弃
SwitchTransformer
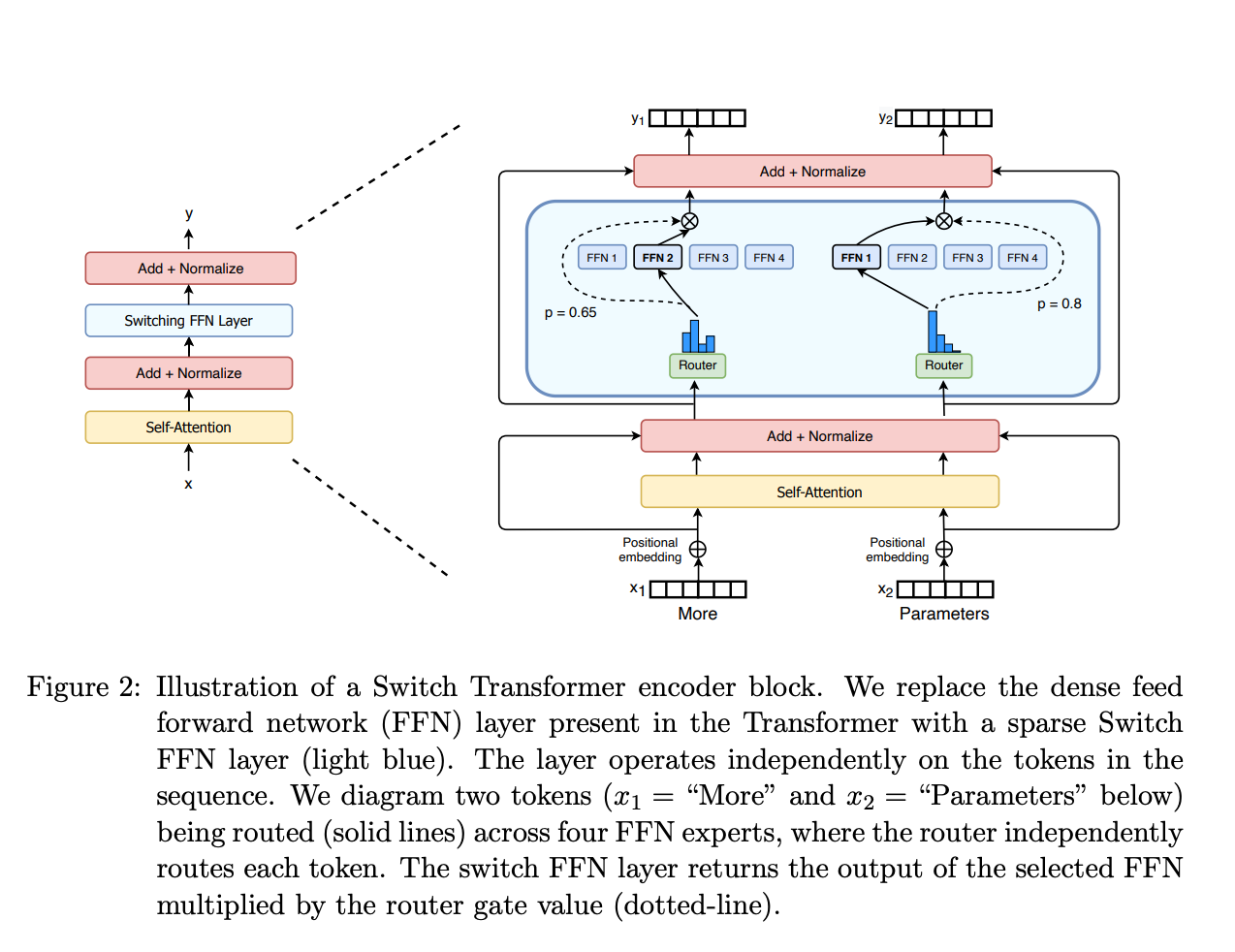
2router + 4expert
通过 Linear 作为 router 计算得到专家下标 然后在共用专家中选择
ST-MoE
router z-loss
$$ L_z(x) = \frac1S\sum_{i=1}^S(\text{log}\sum_{j=1}^E\text{exp}(x_j^{(i)}))^2 $$
$x_j^{(i)}$ 表示 i token 路由到 j expert 的 logit
惩罚门控网络输入的较大 logits
DeepSeek-MoE
V1
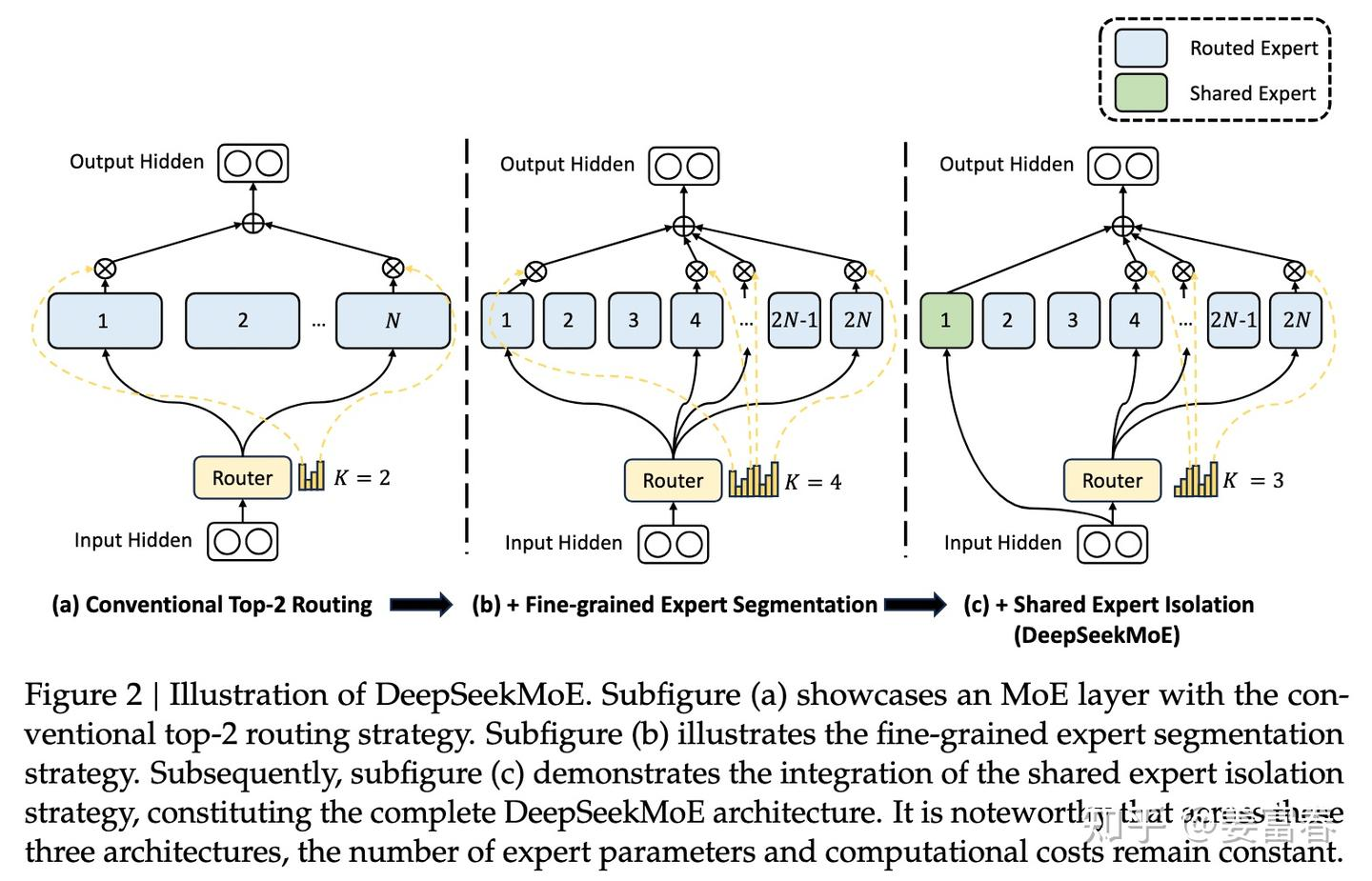
之前问题
- 知识混合: 专家数量少 可能导致学到多类混合知识 不能发挥专业效果
- 知识冗余: 分配给不同专家相同知识 阻碍了专家专业性
架构优化
- 细粒度专家分割 (Fine-Grained Expert Segmentation) 在保持参数数量不变的情况下 作者通过分割FFN中间隐藏维度来将专家分割成更细的粒度 (MLP:[N,4N,N] = 4x MLP:[N,2N,N])
- 共享专家隔离 (Shared Expert Isolation) 将某些专家隔离出来 作为始终激活的共享专家 旨在捕获不同上下文中的共同知识
$$ h_t^l = \sum_{i=1}^{K_s}\text{FFN}_i (u_t^l) + \sum_{i=K_s+1}^{mN}(g_{i,t}\text{FFN}_i (u_t^l)) + u_t^l $$
- $K_s$ 个共享专家
- $mN-K_s$ 个路由专家
- $u_t^l$ 是 $l$ 层 $t$ token 输入
- $g_{i,t}$ 是 TopK 专家权重
- $s_{i,t} = \text{Softmax}_i(u_t^{lT}e_i^l)$ 专家得分
Expert-level balance loss
$$ \mathcal{L}_\text{ExpBal} = \alpha_1\sum_{i=1}^{N’}f_iP_i $$
- $f_i=\frac{N’}{K’T}\sum_{t=1}^T\Bbb{I}(\text{Token } t \text{ selects Expert } i)$
- $T$ 全部token数
- $N’=mN-K_s$ 去掉共享专家后的路由专家的数量
- $K’=mK-K_s$ 激活路由专家的数量
- $\Bbb{I}$ 指示函数
- $P_i=\frac{1}{T}\sum^T_{t=1}s_{i,t}$
$\frac{N’}{K’}$ 是为了保持计算损失的恒定 不随专家数量的变化而变化
在token平均分配的情况下 $f_i=K’/N’,\; P_i=\frac1T\times \frac{TK’}{N’}=1/N’,\; \sum f_iP_i=K’/N'$
Device-level balance loss
$$ \mathcal{L}_\text{DevBal} = \alpha_2\sum_{i=1}^{D}f’_iP’_i $$ $$ f’_i=\frac{1}{|\varepsilon_i|}\sum_{j\in\varepsilon_i}f_i $$ $$ P’_i=\sum_{j\in\varepsilon_i}P_j $$
划分专家为D组
V2
Device-limited routing
保证每个token的激活专家 最多发布到 M (M < K) 个设备上
- 先计算门控分数最高专家所在的M个设备
- 再从M设备的专家中选择TopK
DeepSeek V2: K=6, M=3
Communication balance loss
$$ \mathcal{L}_\text{CommBal} = \alpha_3\sum_{i=1}^{D}f’’_iP’’_i $$ $$ f’’_i=\frac{D}{MT}\sum_{t=1}^T\Bbb{I}(\text{Token } t \text{ is sent to Device } i) $$ $$ P’’_i=\sum_{j\in\varepsilon_i}P_j $$
跟专家负载均衡差不多
Token-dropping strategy
丢掉超过容量的token (MoE层不计算)
V3
GLM4-MoE 使用同样架构
MoE使用Sigmoid作为门控函数 (提高区分度)
Auxiliary loss free load balancing
去掉了之前一堆balance loss
设置bias 通过 $s_{i,t}+b_i$ 来选取 TopK
Complementary sequence-wise auxiliary loss
$$ \mathcal{L}_\text{ExpBal} = \alpha_1\sum_{i=1}^{N’}f_iP_i $$ $$ f_i=\frac{N’}{K’T}\sum_{t=1}^T\Bbb{I}(\text{Token } t \text{ selects Expert } i) $$ $$ s’_{i,t}=\frac{s_{i,t}}{\sum_{j=1}^{N’}s_{i,t}} $$ $$ P_i=\frac{1}{T}\sum^T_{t=1}s’_{i,t} $$
sequence粒度的负载均衡损失 对得分norm了一下
(去掉了token drop)
LongCat-MoE
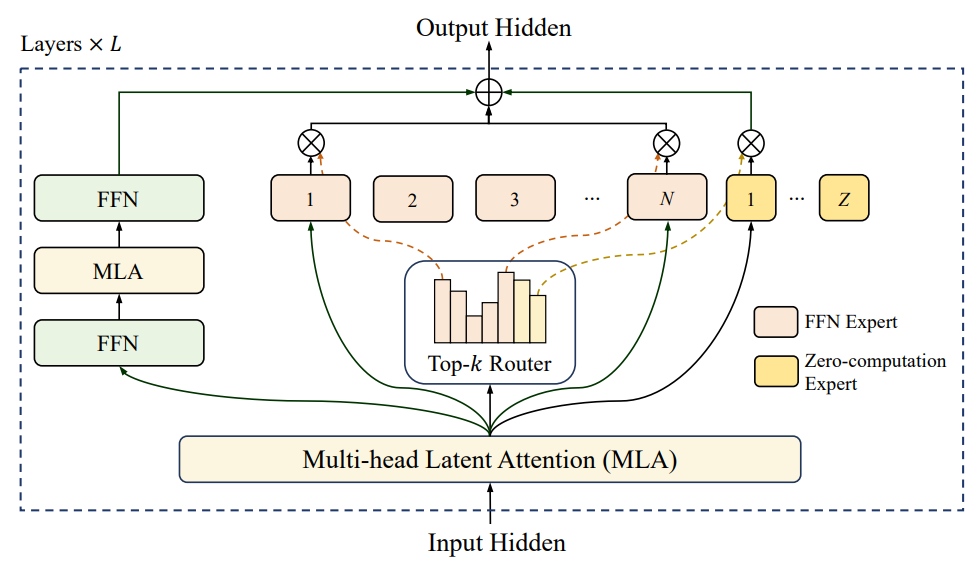
- Zero-computation Experts: 减少参数量
- Shortcut-connected MoE: 减少计算量 提高推理效率
$$ \text{MoE}(x_t) = \sum_{i=1}^{N+Z} g_i E_i(x_t), $$
$$ g_i = \begin{cases} R(x_t)_i, & \text{if } R(x_t)_i \in \mathrm{TopK}(R(x_t)_i + b_i \mid 1 \le i \le N+Z, K), \\ 0, & \text{otherwise}, \end{cases} $$
$$ E_i(x_t) = \begin{cases} \text{FFN}_i(x_t), & \text{if } 1 \le i \le N, \\ x_t, & \text{if } N < i \le N+Z, \end{cases} $$
- Z: 零计算专家数量
- N: 标准专家数量
- R: softmax router
- K: 激活专家数
- $b_i$: expert bias
Computational budget control
使用 aux-loss-free stratege
expert bias 每步更新如下
$$ \Delta b_i = \begin{cases} \mu(\frac{K_e}{K}\cdot\frac{1}{N}-\frac{T_i}{KT_{all}}), &\text{if } 1\le i \le N \\ 0,&\text{if } N\lt i \le N+Z \end{cases} $$
- $T_{all}$: 一个batch的token数量
- $T_i$: 路由到 $E_i$ 专家的token数
- $K_e$: 期望激活专家
Load balance control
划分 N 个专家为 D 得到 $G=\frac{N}{D}$
$$ \mathcal{L}_{\text{LB}} = \alpha \sum_{j=1}^{D+1} f_j P_j, \\ P_j = \frac{1}{T} \sum_{i \in \text{Group}_j} \sum_{t=1}^{T} R(x_t)_i, \\ f_j = \begin{cases} \frac{D}{K_e T} \sum_{t=1}^{T} \mathbb{I}(\text{token } t \text{ selects Group}_j), & \text{if } 1 \le j \le D, \\ \frac{1}{(K - K_e) T} \sum_{t=1}^{T} \mathbb{I}(\text{token } t \text{ selects zero-computation experts}), & \text{if } j = D+1, \end{cases} $$
T: micro batch 的token数
将所有的零计算专家分到一组