简单介绍强化学习中的 Markov * 内容
Markov
Markov property
一个随机过程在给定现在状态及所有过去状态情况下,其未来态的条件概率分布仅依赖于当前状态
(另一种描述) 给定当前状态时 将来的状态与过去的状态条件独立
对于离散随机过程
$$ p(X_{t+1}=x_{t+1}|X_{0:t}=x_{0:t}) = p(X_{t+1}=x_{t+1}|X_t=x_t) $$
随机变量的所有可能取值的集合为状态空间(state space)
Markov process
一组具有 Markov property 的随机变量序列 下一个状态只取决于当前状态
随机序列 $s_1, …, s_t$ 状态历史 $h_t={s_1,…,s_t}$
马尔科夫过程满足 $p(s_{t+1}|s_t)=p(s_{t+1}|h_t)$
离散时间的马尔科夫过程被成为马尔科夫链
可以用状态转移矩阵 P 描述 上面的状态转移
$$ P = \begin{pmatrix} p(s_1|s_1) & p(s_2|s_1) & \cdots & p(s_N|s_1) \ p(s_1|s_2) & p(s_2|s_2) & \cdots & p(s_N|s_2) \ \vdots & \vdots & \ddots & \vdots \ p(s_1|s_N) & p(s_2|s_N) & \cdots & p(s_N|s_N) \ \end{pmatrix} $$
Markov reward process
MRP=MP+reward_function
reward/value-function
一些概念
- 范围(horizon): 一个回合的长度
- 回报(return):
- 把奖励进行折扣后所获得的奖励
- 可定义为奖励的逐步叠加
- $G_t=\sum_{i=t}^{T-1}{\gamma^{i-t}r_{t+1}}$
状态价值函数: V-function = state-value function
$$ V^t(s) = E[G_t|s_t=s] $$
Bellman equation
定义了状态之间的迭代关系
$$ V(s)=\underset{\text{instant reward}}{R(s)} + \underset{\text{dicounted sum of future reward}}{\gamma\sum_{s’\in S}p(s’|s)V(s’)} $$
仿照全期望公式可证明 $$ E[V(s_{t+1})|s_t]=E[E[G_{t+1}|s_{t+1}]|s_t]=E[G_{t+1}|s_t] $$
即 $$ \begin{align*} V(s) & = E[G_t|s_t=s] \ & = E[\sum_{i=t}^{T-1}{\gamma^{i-t}r_{t+1}}|s_t=s] \ & = E[r_{t+1}|s_t=s] + \gamma E[r_{t+2}+…|s_t=s] \ & = R(s) + \gamma E[G_{t+1}|s_t=s] \ & = R(s) + \gamma E[V(s_{t+1})|s_t=s] \ & = R(s) + \gamma\sum_{s’\in S}p(s’|s)V(s’) \end{align*} $$
可以写成矩阵形式
$$ \begin{align} V & = R + \gamma PV \ IV & = R + \gamma PV \ (I-\gamma P)V & = R \ V & = (I - \gamma P)^{-1}R \end{align} $$
可以直接获得V函数的解析解
Markov Decision Process
MDP = MRP + action
$$ p(s_{t+1}|s_t,a_t) = p(s_{t+1}|h_t,a_t) \ R(s_t=s,a_t=a) = E[r_t|s_t=s,a_t=a] $$
D in MDP
策略定义了在具体状态下该采取的动作 $\pi(a|s)=p(a_t=a|s_t=s)$
如果决策过程和策略$\pi$确定 马尔科夫决策过程可以转换成马尔科夫奖励过程
在决策过程中 状态转移函数 $p(s’|s,a)$ 可以去掉 $a$
$$ p_\pi(s’|s) = \sum_{a\in A}\pi(a|s)p(s’|s,a) $$
对于奖励函数
$$ R_\pi(s) = \sum_{a\in A}\pi(a|s)R(s,a) $$
Markov-diff
MDP 在状态转移函数上面对一个参数: 动作$a$
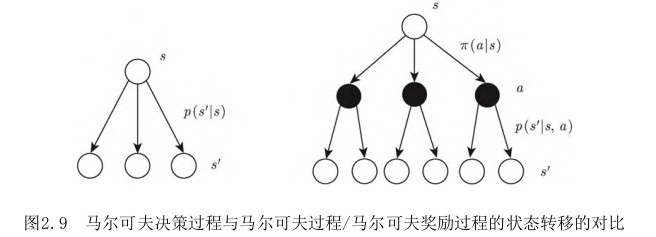
在MDP中 动作由agent给出
decision/value-function
基于策略的状态价值: $V_\pi(s) = E_\pi[G_t|s_t=s]$
动作价值函数: Q-function = action-value function
$$ Q_\pi(s,a) = E_\pi[G_t|s_t=s, a_t=a] $$
马尔科夫决策过程的回报期望是基于策略函数的 价值函数如下
$$ V_\pi(s) = \sum_{a\in A}\pi(a|s)Q_\pi(s,a) $$
推导Q函数的Bellman-equation
$$ \begin{align*} Q(s,a) & = E[G_t|s_t=s, a_t=a] \ & = … & = R(s,a) + \gamma E[G_{t+1}|s_t=s,a_t=a] \ & = R(s,a) + \gamma E[V(s_{t+1})|s_t=s,a_t=a] \ & = R(s,a) + \gamma\sum_{s’\in S}p(s’|s,a)V(s’) \end{align*} $$
Bellman expectation equation
定义了当前状态与未来状态之间的关联
把V函数和Q函数拆解为 即时奖励和后续状态的折扣奖励
$$ \begin{cases} V_\pi(s) = E_\pi[r_{t+1}+\gamma V_\pi(s_{t+1})|s_t=s] & \text{分解V函数} \ V_\pi = \sum_{a\in A}\pi(a|s)\left(R(s,a) + \gamma\sum_{s’\in S}p(s’|s,a)V_\pi(s’)\right) \end{cases} $$ $$ \begin{cases} Q_\pi(s,a) = E_\pi[r_{t+1}+\gamma Q_\pi(s_{t+1},a_{t+1})|s_t=s,a_t=a] & \text{分解Q函数} \ Q_\pi(s,a) = R(s,a) + \gamma \sum_{s’\in S}p(s’|s,a)\sum_{a’\in A}\pi(a’|s’)Q_\pi(s’,a’) \end{cases} $$
最后两个式子都是贝尔曼期望方程的另一种形式
value-prediction
计算价值函数 $V_\pi(s)$ 的过程就是 策略评估 也被称为 价值预测 (预测策略最终的价值)
prediction-control
预测和控制是马尔科夫决策过程中的核心问题
预测(计算每个状态的价值): $<S, A, P, R, \gamma>,+,\pi \to V_\pi$
控制(搜索最佳策略): $<S, A, P, R, \gamma>\to V^,+,\pi^$
通过解决预测问题 进而解决控制问题
马尔科夫决策过程控制
最佳价值函数和最佳策略定义
$$ V^(s) = \underset{\pi}{max}V_\pi(s) \ \pi^(s) = \underset{\pi}{argmax}V_\pi(s) \ \pi^(a|s) = \begin{cases} 1, & a=\underset{\pi}{argmax}Q^(s,a) \ 0, & others \end{cases} $$
搜索最佳策略有两种常用方法
- 策略迭代
- 价值迭代
| 问题 | 贝尔曼方程 | 算法 |
|---|---|---|
| 预测 | 贝尔曼方程 | 迭代策略评估 |
| 控制 | 贝尔曼期望方程 | 策略迭代 |
| 控制 | 贝尔曼最优方程 | 价值迭代 |
策略迭代
策略迭代两个步骤
- 策略评估: 给定策略函数估计状态价值函数
- 策略改进: 得到状态价值函数 推算Q函数并最大化 通过对Q函数贪心搜索改进策略
Bellman optimality equation
$$ V_\pi(s) = \underset{a\in A}{max}Q_\pi(s,a) $$
最佳策略下的一个状态的价值必须等于在这个状态下采取最好动作得到的回报的期望
价值迭代
最优性原理定理(priciple of optimality theorem): 一个策略在某状态达到最优价值当且仅当对于任何能够从某状态到达的状态都已经达到了最优价值
$$ V_\pi(s)=V^(s) \Leftrightarrow V_\pi(s’)=V^(s’) $$